数学与音乐的奇妙共振：巧妙掌握，事半功倍！

节奏：音乐的骨骼，数学的脉搏

1. 节奏的数学本质

节奏是音乐中时间流逝的组织方式，它决定了音符出现的规律和频率。这种规律和频率可以用数学比率来精确地描述。例如，一个4/4拍的乐曲，意味着每小节有四个四分音符。不同的音符时值（全音符、二分音符、四分音符等）之间的比例关系，都可以用简单的数学分数来表示。我记得小时候学习钢琴时，老师总是强调数拍子的重要性，当时觉得很枯燥，但现在回想起来，才明白这其实就是在学习音乐中的数学规律。我自己也尝试过用不同的数学比率来创作简单的节奏，发现即使是最简单的数学公式，也能产生意想不到的音乐效果。

2. 节奏与情感表达

节奏不仅仅是数学的体现，它也是情感表达的重要手段。不同的节奏可以营造出不同的氛围和情感。例如，快速的节奏通常表达兴奋、激动或紧张的情绪，而缓慢的节奏则表达平静、忧伤或庄严的情绪。我曾经听过一场音乐会，其中一首曲子使用了非常复杂的节奏变化，时而快速激烈，时而缓慢舒缓，完美地展现了作曲家想要表达的内心挣扎和情感转变。节奏的运用，让音乐不再只是音符的堆砌，而是成为了一种充满生命力的艺术。

3. 现代音乐中的节奏创新

在现代音乐中，节奏的运用变得越来越多样化和复杂化。许多作曲家开始尝试使用非传统的节奏模式，例如不规则的节拍、复节奏等，以创造出更加新颖和独特的音乐效果。一些电子音乐制作人甚至会利用数学算法来生成节奏，创造出以前难以想象的音乐结构。我最近在网上看到一些用程序生成的音乐，节奏非常复杂，但却充满了活力和创意，让我不得不感叹数学与音乐结合的无限可能性。

音高：旋律的灵魂，频率的化身

1. 音高的数学定义

音高是指声音的高低，它是由声音的频率决定的。频率越高，音高越高；频率越低，音高越低。在音乐中，不同的音符对应着不同的频率。例如，标准音A（A4）的频率为440Hz。音阶中的各个音符之间的频率关系，可以用数学比例来精确地描述。例如，纯八度音程的频率比为2:1，纯五度音程的频率比为3:2。我记得以前学习音乐理论时，对这些频率比例感到非常头疼，但当我开始用频谱分析仪来观察不同乐器的音高时，我才真正理解了这些数学关系的实际意义。

2. 和谐与不和谐的数学解释

有些音程听起来和谐悦耳，而有些音程则听起来刺耳不和谐。这种和谐与不和谐的感觉，可以用数学比例来解释。当两个音符的频率比是简单的整数比时，它们听起来通常比较和谐，例如八度（2:1）、五度（3:2）和四度（4:3）。而当频率比是复杂的无理数时，它们听起来通常比较不和谐，例如增四度和减五度。我曾经做过一个实验，用软件生成不同频率比例的音程，然后让朋友们来评价它们的和谐程度，结果与数学理论的预测基本一致。这让我更加确信，音乐的和谐与不和谐，并非完全是主观感受，而是有其客观的数学基础。

3. 音高与文化差异

虽然音高的数学基础是普遍适用的，但不同文化对音高的理解和运用却存在差异。例如，在西方音乐中，十二平均律是一种常用的音高体系，它将一个八度音程平均分成十二个半音。而在一些东方音乐中，则使用更加复杂的音高体系，例如中国的五声音阶和印度的微分音。我曾经听过一场印度古典音乐会，其中一位演奏家使用了一种叫做“shruti”的微分音技巧，将音高细微地变化，创造出一种非常独特的音乐效果。这让我意识到，音乐的魅力不仅在于其数学的精确性，还在于其文化的丰富性。

和声：音符的协奏，数学的共振

1. 和弦的数学构成

和声是指多个音符同时发声所产生的效果。和弦是和声的基本单位，它由三个或三个以上的音符组成。不同的和弦具有不同的音响效果，例如大和弦通常听起来明亮、积极，而小和弦则通常听起来忧郁、消极。和弦的构成可以用数学来描述。例如，一个C大三和弦由C、E、G三个音符组成，它们之间的音程关系为大三度和小三度。我曾经尝试用不同的数学公式来生成和弦，发现即使是最简单的公式，也能产生意想不到的和声效果。这种探索让我更加体会到数学在音乐创作中的重要作用。

2. 和声进行与情感变化

和声进行是指一系列和弦按照一定的顺序排列所产生的效果。不同的和声进行可以营造出不同的情感氛围。例如，从主和弦到属和弦再回到主和弦（I-V-I）是一种常见的和声进行，它通常表达一种稳定、安全的感觉。而一些复杂的和声进行则可以表达更加复杂的情感，例如紧张、冲突、释放等。我曾经分析过一些我喜欢的歌曲的和声进行，发现作曲家们常常会巧妙地运用和声进行来表达歌曲的情感主题。这种分析让我更加深入地理解了音乐的结构和表达方式。

3. 现代音乐中的和声探索

在现代音乐中，作曲家们对和声的探索变得越来越大胆和创新。他们开始尝试使用不协和的和弦、非传统的和声进行等，以创造出更加新颖和独特的音乐效果。一些作曲家甚至会利用数学算法来生成和声，创造出以前难以想象的音乐结构。我最近在网上看到一些用程序生成的音乐，和声非常复杂，但却充满了惊喜和创意，让我不得不感叹数学与音乐结合的无限可能性。这种探索也让我更加期待未来音乐的发展方向。

音乐元素	数学概念	联系	例子
节奏	比率、分数、模式	时间的组织方式，音符时值的比例	4/4拍，3/4拍
音高	频率、对数、比例	声音的高低，音阶中音符的频率关系	标准音A（440Hz），八度音程（2:1）
和声	集合论、函数、转换	多个音符同时发声的效果，和弦的构成	C大三和弦（C-E-G），I-V-I和声进行
音色	傅里叶分析、谐波、频谱	声音的色彩，不同乐器的频谱特征	不同乐器的音色差异

音色：乐器的个性，波形的指纹

1. 音色的物理特性

音色是指声音的色彩，它是由声音的波形决定的。不同的乐器发出声音的波形不同，因此它们的音色也不同。音色可以用傅里叶分析来描述，它将一个复杂的波形分解成一系列简单的正弦波，每个正弦波都有自己的频率和振幅。这些频率和振幅的组合构成了声音的频谱，而频谱就是音色的“指纹”。我曾经用软件分析过不同乐器的音色，发现即使是同一种乐器，在不同的演奏方式下，它们的频谱也会发生变化。这让我更加深入地理解了音色的复杂性和多样性。

2. 音色与情感表达

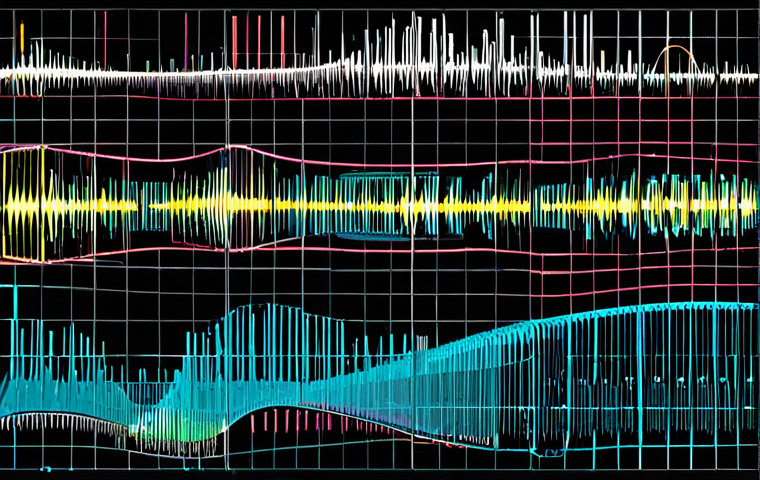
音色不仅仅是物理的特性，它也是情感表达的重要手段。不同的音色可以营造出不同的氛围和情感。例如，小提琴的音色通常表达温柔、浪漫的情绪，而吉他的音色则通常表达奔放、自由的情绪。作曲家们常常会根据作品的情感主题来选择不同的乐器，以达到最佳的表达效果。我曾经听过一场交响乐音乐会，其中一位作曲家巧妙地运用了不同乐器的音色，将乐曲的情感层次表达得淋漓尽致。这让我意识到，音色在音乐中的作用远不止于美化声音，它更是情感表达的重要组成部分。

3. 数字音色与合成器

随着数字技术的发展，数字音色和合成器在音乐创作中扮演着越来越重要的角色。合成器可以模拟各种乐器的音色，甚至可以创造出以前从未有过的音色。数字音色可以通过算法来精确地控制，从而创造出更加新颖和独特的音乐效果。我最近在网上看到一些用合成器制作的音乐，音色非常丰富，充满了未来感和科技感，让我不得不感叹数字技术在音乐创作中的巨大潜力。数字音色和合成器的出现，为音乐创作打开了全新的可能性。

结构：乐曲的蓝图，逻辑的延伸

1. 音乐结构的数学模型

音乐结构是指乐曲的整体组织方式，它包括乐句、乐段、乐章等不同的层次。音乐结构可以用数学模型来描述。例如，赋格曲是一种常见的音乐结构，它由一个主题和多个模仿声部组成，这些声部按照一定的规则进行交织和叠加。奏鸣曲式是另一种常见的音乐结构，它由呈示部、展开部和再现部组成，这些部分按照一定的逻辑顺序进行排列。我曾经学习过一些音乐分析的课程，发现许多经典的乐曲都遵循着某种数学的结构，例如黄金分割比例、斐波那契数列等。这让我更加相信，音乐结构并非完全是偶然的，而是有其内在的数学逻辑。

2. 对称与重复在音乐中的应用

对称和重复是音乐结构中常用的手法。对称是指乐曲的某些部分在时间上或音高上呈现对称关系，例如回旋曲式和卡农。重复是指乐曲的某些部分在不同的地方重复出现，例如主题和变奏。这些手法可以增强乐曲的统一性和连贯性，使听众更容易理解和记忆。我曾经分析过一些我喜欢的歌曲的结构，发现作曲家们常常会巧妙地运用对称和重复的手法，使歌曲的结构更加清晰和有力。这种分析让我更加深入地理解了音乐的组织方式和表达效果。

3. 现代音乐中的结构解构

在现代音乐中，作曲家们对音乐结构的解构变得越来越普遍。他们开始尝试打破传统的结构模式，例如不规则的乐句、非线性的发展等，以创造出更加新颖和独特的音乐效果。一些作曲家甚至会利用随机算法来生成音乐结构，创造出以前难以想象的音乐形式。我最近在网上看到一些用程序生成的音乐，结构非常混乱，但却充满了实验性和挑战性，让我不得不感叹现代音乐的无限可能性。这种解构也让我更加期待未来音乐的发展方向。

音乐与数学的融合：无限的可能

1. 算法音乐：数学的直接表达

算法音乐是指利用数学算法来创作音乐的一种形式。算法音乐可以生成各种各样的音乐，从简单的旋律到复杂的交响乐。算法音乐的优点在于它可以创造出以前难以想象的音乐结构，同时也可以让音乐创作更加自动化和智能化。我曾经尝试用一些算法音乐软件来创作音乐，发现即使是我这个不懂音乐的人，也能创作出一些有趣的音乐作品。这让我更加相信，算法音乐将会在未来音乐创作中扮演越来越重要的角色。

2. 数据可视化音乐：感官的延伸

数据可视化音乐是指将数据转化为音乐的一种形式。数据可视化音乐可以将各种各样的数据，例如股票价格、天气预报、社交媒体数据等，转化为音乐，从而让人们以一种新的方式来感知和理解数据。我曾经听过一些数据可视化音乐作品，其中一些作品将股票价格的变化转化为音高的变化，另一些作品将天气预报转化为节奏的变化。这些作品让我感到非常新奇和有趣，同时也让我意识到，音乐不仅仅是一种艺术形式，更是一种信息传递的手段。

3. 人工智能音乐：未来的趋势

随着人工智能技术的发展，人工智能音乐成为了一个备受关注的领域。人工智能音乐可以学习人类的音乐风格，并在此基础上创作出新的音乐作品。人工智能音乐的优点在于它可以快速生成大量的音乐，同时也可以为音乐创作提供新的灵感。我最近在网上看到一些人工智能创作的音乐作品，其中一些作品已经达到了专业水平，甚至可以与人类作曲家相媲美。这让我相信，人工智能音乐将会在未来音乐创作中扮演越来越重要的角色，甚至可能会彻底改变音乐的创作和欣赏方式。

文章结尾

音乐与数学的结合，远不止于理论的推导和公式的运用。它更是一种对世界的深刻理解和感性表达。通过数学的视角，我们能够更深入地认识音乐的本质，而通过音乐的体验，我们也能更好地领悟数学的魅力。这种跨学科的融合，为我们开启了一扇通往无限可能的大门。希望这篇文章能引发您对音乐和数学更深层次的思考。

实用小贴士

1. 学习基础乐理知识：了解音符、节奏、和弦等基本概念，为深入理解音乐的数学本质打下基础。

2. 尝试创作简单的音乐：利用一些音乐创作软件或工具，尝试创作简单的旋律或节奏，体验数学在音乐创作中的应用。

3. 分析喜欢的音乐作品：选择一些自己喜欢的音乐作品，分析其节奏、音高、和声等元素，深入理解音乐的结构和表达方式。

4. 探索算法音乐和数据可视化音乐：了解算法音乐和数据可视化音乐的概念和应用，感受数学在音乐领域的创新和发展。

5. 关注音乐与数学相关的研究：阅读相关书籍、文章或报告，了解音乐与数学领域最新的研究成果和发展趋势。

要点总结

节奏是音乐中时间流逝的组织方式，可以用数学比率来描述。

音高是指声音的高低，由声音的频率决定，可以用数学比例来精确地描述。

和声是指多个音符同时发声所产生的效果，和弦的构成可以用数学来描述。

音色是指声音的色彩，由声音的波形决定，可以用傅里叶分析来描述。

音乐结构是指乐曲的整体组织方式，可以用数学模型来描述。